第一学时(45分钟)
1.导入(5分钟)
提问:袋中有
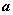 只白球, 只白球,
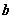 只红球,做有放回抽样,每次取一只,问:第一次取到白球的概率是多少?第二次取到白球的概率是多少? 只红球,做有放回抽样,每次取一只,问:第一次取到白球的概率是多少?第二次取到白球的概率是多少?
引导学生思考事件之间的关系,引发学生的学习兴趣,从而导入新课----事件的独立性。
2.概念讲解(15分钟)
1)给出两个事件
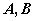 相互独立的概念: 相互独立的概念: 设
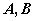 为两事件,若 为两事件,若
 ,则称 ,则称
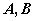 相互独立。结合导入的例子,详细解释公式中每个概率的含义,说明当满足等式时,两事件发生与否不会相互影响,反之亦然。 相互独立。结合导入的例子,详细解释公式中每个概率的含义,说明当满足等式时,两事件发生与否不会相互影响,反之亦然。
2)通过抛两枚硬币的简单例子,进一步说明事件独立性。
3.讲解性质与课堂练习(25分钟)
若
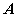 与 与
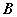 相互独立,则 相互独立,则
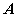 与 与
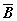 , ,
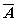 与 与
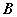 , ,
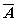 与 与
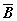 均相互独立。引导学生思考:从简单实例解答,例如两个人同时投篮,互相不收影响投中与否无关,所以是独立的。后面学习中如果涉及到产品很多,从中抽取一个做抽样,由于抽取的相对少,不放回与有放回实验的差距不大,此时理论上的不放回也可看做是独立的,给问题的研究带来方便。 均相互独立。引导学生思考:从简单实例解答,例如两个人同时投篮,互相不收影响投中与否无关,所以是独立的。后面学习中如果涉及到产品很多,从中抽取一个做抽样,由于抽取的相对少,不放回与有放回实验的差距不大,此时理论上的不放回也可看做是独立的,给问题的研究带来方便。
知识拓展:三个事件两两相互独立如何定义?
实例:甲、乙两人独立射击同一目标,他们击中的概率分别为0.9和0.8,求在一次射击中目标被击中的概率?
让学生独立思考并解答,及时纠正学生的错误思路和解答过程,选取学生代表回答,教师进行点评和总结。
通过本例说明:一起开火击中概率增加,以数学建模竞赛为例,一组三人,要通过分工协作,才能获得最后的胜利。此处巧妙引入课程思政,提醒学生要注意培养团队合作意识,并为目标努力奋斗。
|

