课题名称

高等数学

授课教师

范小丹

授课对象

材料与新能源材料专业本科生一年级

课程性质

通识与公共基础必修课

   教学内容：3.7 曲率

教学说明和教学理念        

 本章节重点介绍曲率相关知识，包括弧微分概念，曲率的定义、计算，以及曲率圆和曲率半径。教学中注重理论联系实际，通过实例和几何直观帮助学生理解抽象概念，培养学生运用数学知识解决实际问题的能力，让学生体会高等数学在工程和科学领域的重要应用。                

1.以学生为中心，关注学生从直观感知到抽象理解的认知发展，兼顾知识学习、思维训练和应用能力提升。        

2.强调理论与实践结合，用实际问题引出数学概念，再将理论应用于解决实际问题。        

3.融合数学与工程、物理等学科知识，构建跨学科知识体系，提升学生解决复杂问题的能力。

 教学设计总体思路        

1.充分准备：课前精心梳理教学内容，制作生动的多媒体课件，准备相关视频、图片和工程案例。分析学生知识基础和学习特点，设计针对性的问题和练习。准备数学软件演示曲率动态变化过程，提升教学直观性。      

2.诱发与释疑：通过赛道、公路、铁轨弯道等实际例子引入，引发学生对曲线弯曲程度度量的思考。运用动画展示曲线变化，结合类比、比喻解释抽象概念。设置问题引导学生分步骤思考，逐步深入理解知识。

3.转化与应用：课堂上安排适量例题和练习，让学生即时应用知识，巩固理解。鼓励学生在课后寻找生活中可应用曲率知识的场景，分析解决问题，真正做到学以致用。        

4.思政融入：通过介绍陈立泉院士呕心沥血、精益求精、锐意创新、淡泊名利坚守电池研究 40 余年的事迹，激励学生的钻研精神、工匠精神和严谨治学的态度。        

5.拓展与延伸：提供拓展阅读材料，如曲率在计算机图形学、机械设计中的应用案例，拓宽学生视野。组织数学建模小组活动，鼓励学生用曲率知识解决实际建模问题。

   教学主要目标        

1.知识目标：学生掌握弧微分概念及计算，理解曲率定义，熟练运用曲率计算公式，掌握曲率圆与曲率半径概念及计算。        

2.能力目标：通过推理曲率计算公式，培养学生数学运算能力；通过曲线的曲率与曲率圆和曲率半径的关系，培养学生逻辑推理能力；通过应用知识解决实际问题，提升学生数学建模和问题解决能力。

3.情感目标：通过实际案例，让学生感受数学的实用性和魅力，激发学生对高等数学的学习兴趣；通过解决复杂问题，培养学生勇于探索、克服困难的精神。        

教学重点与难点 

重点：曲率计算公式推导与计算、曲率圆和曲率半径概念理解。      

难点：曲率概念的直观理解、曲率计算公式推导及在复杂曲线中的应用。

解决重点与难点的方法

1.理论联系实际：借助大量实际案例，如赛道的弯道、公路与铁路的弯道设计，锂电池电极材料、光伏材料的应用，帮助学生理解抽象概念。引导学生运用所学知识分析实际问题，实现知行合一。

2.可视化教学：利用动画、图形展示曲线弯曲程度变化、曲率圆动态生成等过程，增强直观感受。使用数学软件绘制曲线及曲率相关图形，辅助学生理解。

3.分步引导：推导曲率计算公式时，将复杂过程分解为多个步骤，逐步引导学生思考，掌握推导方法。

采用主要教学手段

1.结合传统板书推导公式、讲解重点，与多媒体展示图形、动画、案例，增强教学直观性和趣味性。

2.运用数学软件绘制曲线及曲率圆相关图形，动态演示变化过程。      

3.应用雨课堂开展课堂提问和练习，及时了解学生学习情况，给予反馈和指导。

教学环节—问题导入

（5分钟） 

教学内容：展示韩国速滑名将的失误视频引起学生注意到赛道的弯道设计，给出公路弯道、铁路弯道等图片，引出曲线弯曲程度不同的现象。提出问题：道路弯道设计需考虑什么？如何定量描述曲线的弯曲程度？引出离心力的公式进而引出曲率圆的半径的概念。        

教学设计：先展示图片，让学生观察并描述曲线弯曲特点。然后提出问题，组织简单讨论，鼓励学生分享想法。通过生活实例引导学生初步认识到研究曲线弯曲程度的必要性，激发学生对新知识的好奇心和探索欲望。

教学环节—弧微分讲解

（10分钟）

教学内容：从曲线长度计算引出弧微分概念，推导弧微分公式

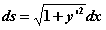教学设计：先回顾曲线长度近似计算方法，逐步引出弧微分概念。在黑板上详细推导直角坐标下弧微分公式，每一步讲解推导思路和依据。为下一步推导曲率公式打下基础。

教学环节—曲率及其计算公式讲解

（30分钟）

教学内容：给出曲率定义，从直观角度解释曲率表示曲线弯曲程度；详细推导曲率计算公式 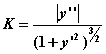；通过具体函数实例应用公式计算曲率。
教学设计：结合弯曲道路驾驶感受，类比引入曲率定义，帮助学生直观理解。在黑板上逐步推导曲率计算公式，边推导边提问引导学生思考，如“为什么要这样变形”、“这一步用到了什么知识”等。推导完成后，给出简单函数，示例求曲线的曲率。然后让学生计算某点处曲率，展示答题结果，教师点评总结，强调计算要点和易出错地方。

教学环节—曲率圆与曲率半径讲解

（20分钟）

教学内容：讲解曲率圆和曲率半径概念，说明其与曲线在某点处弯曲程度关系；介绍曲率圆性质，如与曲线在该点有相同切线、曲率等；通过实际例子（如铁轨弯道设计）说明曲率圆和曲率半径应用。

教学设计：利用动画展示曲率圆在曲线上某点生成过程，结合图形讲解概念和性质。通过铁轨弯道设计案例，从火车行驶平稳需求出发，解释如何根据曲率圆和曲率半径设计铁轨。组织学生思考、讨论，让学生思考生活中还有哪些地方应用到曲率圆和曲率半径知识，通过投稿形式分享，教师补充完善。

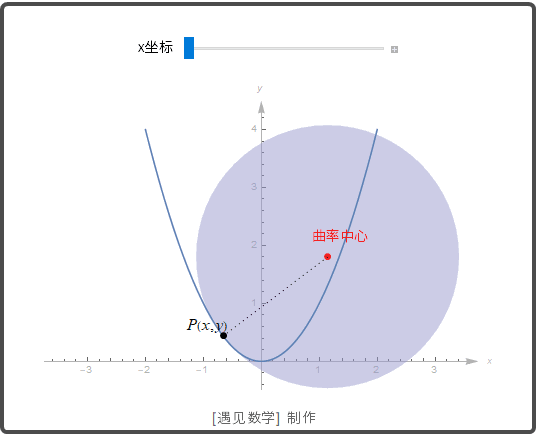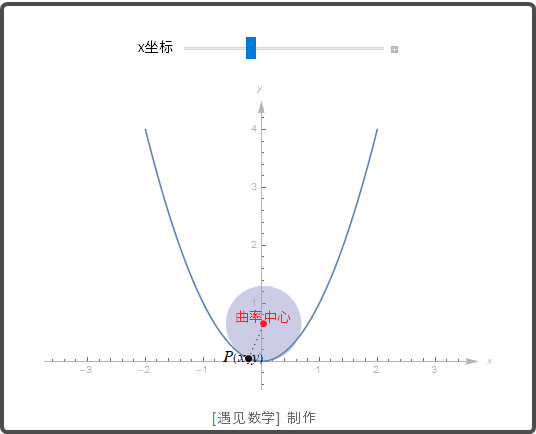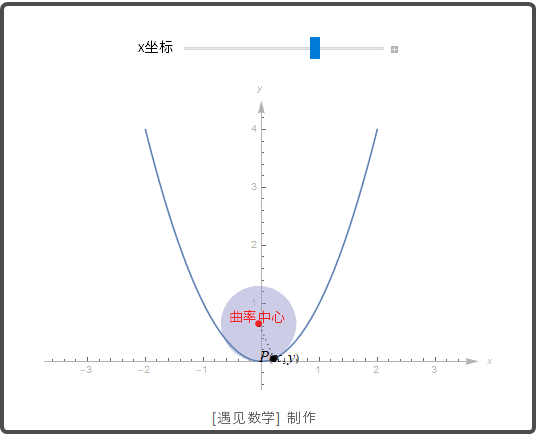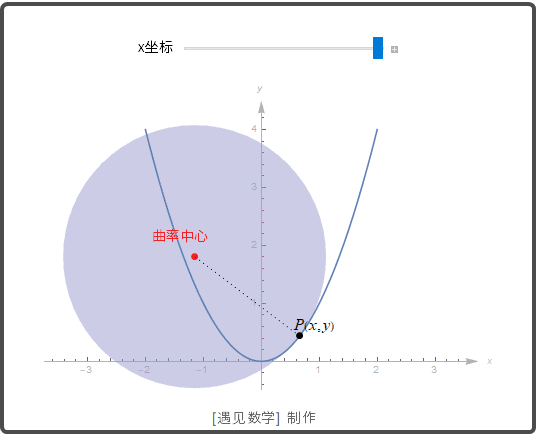
教学环节—巩固加深，提高升华

（15分钟）

教学内容：给出综合性例题，涉及锂电池电极材料和太阳能电池板薄膜变形问题，有关曲率及曲率圆相关计算；引导学生思考曲率知识在本学科的应用。

教学设计：呈现综合性例题，让学生先独立思考、尝试解答。然后请几位学生回答不同解题思路及结果，教师有针对性的进行点评，纠正错误，总结解题方法和技巧。通过提问引导学生联想物理学科中类似曲线弯曲场景，鼓励学生课下查阅资料深入探究，提升知识综合应用能力。

教学环节—总结提高

（10分钟）

1.教师回顾总结本章节主要知识点，包括弧微分、曲率、曲率圆与曲率半径概念及相关公式，强调重点内容和解题关键。        

2.请学生分享本节课学习收获和困惑，教师给予解答和学习建议，布置课后任务。

教学环节—课后任务

1.要求学生整理课堂笔记，总结解题方法；

2.完成课后习题中相关作业题；        

3.可寻找一个生活中能用曲率知识解释的现象，写一篇简短分析报告；  

4.推荐课后学习资料，如《数学分析中的典型问题与方法》中曲率相关拓展内容、数学科普视频《曲线的奥秘：曲率》。